Symmetry Reasoning for Multi-Agent Path Finding

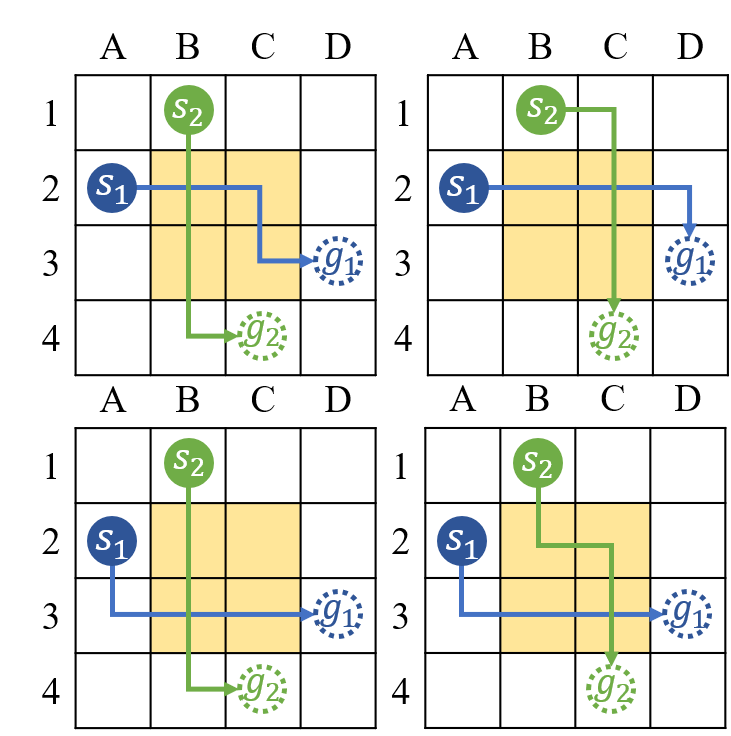
Multi-Agent Path Finding (MAPF) is a challenging combinatorial problem that asks us to plan collision-free paths for team of cooperative agents. One of the reasons MAPF problems are so hard to solve is due to a phenomena called pairwise path symmetry, which occurs when two agents have many equivalent paths, all of which appear promising, but which are pairwise incompatible because they result in a collision. The symmetry arises commonly in practice and can produce an exponential explosion in the space of possible collision resolutions, leading to unacceptable runtimes for currently state-of-the-art MAPF algorithms that employ heuristic search, such as Conflict-based Search (CBS). To break symmetries, we propose a variety of constraint-based reasoning techniques, to detect the symmetries as they arise and to efficiently eliminate, in a single branching step, all permutations of two currently assigned but pairwise incompatible paths.

Manually designed symmetry reasoning techniques:

• Rectangle symmetry arises when two agents attempt to cross each other in an open area but all pairs of their shortest paths are in collision;
• Corridor symmetry arises when two agents attempt to pass through the same narrow passage in opposite directions; and
• Target symmetry arises when the shortest path of one agent passes through the target location of a second agent after the second agent has already arrived at it.

Mutex propagation

Symmetry reasoning for k-robust MAPF