Foundations of Multi-Agent Path Finding
 Recent advances in robotics have laid the foundation for building large-scale multi-agent systems. A great deal of research has focused on coordinating agents to fulfill different types of tasks. We focus on one fundamental task - to navigate teams of agents in a shared environment to their goal locations without colliding with obstacles or other agents. One well-studied abstract model for this problem is known as Multi-Agent Path Finding (MAPF). It is defined on a general graph with given start and goal vertices for agents on this graph. Each agent is allowed to wait at its current vertex or move to an adjacent vertex from one discrete timestep to the next one. We are asked to find a path for each agent such that no two agents are at the same vertex or cross the same edge at any timestep (because this would result in a collision). The objective is to minimize the sum of the arrival times of all agents.
Recent advances in robotics have laid the foundation for building large-scale multi-agent systems. A great deal of research has focused on coordinating agents to fulfill different types of tasks. We focus on one fundamental task - to navigate teams of agents in a shared environment to their goal locations without colliding with obstacles or other agents. One well-studied abstract model for this problem is known as Multi-Agent Path Finding (MAPF). It is defined on a general graph with given start and goal vertices for agents on this graph. Each agent is allowed to wait at its current vertex or move to an adjacent vertex from one discrete timestep to the next one. We are asked to find a path for each agent such that no two agents are at the same vertex or cross the same edge at any timestep (because this would result in a collision). The objective is to minimize the sum of the arrival times of all agents.
We push the limits of MAPF solving by developing a variety of AI and optimization techniques to systematically reasoning about the collision-resolution space of the problem. Our optimal, bounded-suboptimal, and suboptimal MAPF algorithms can find solutions for a few hundred, a thousand, and a few thousand agents, respectively, within just a minute. The diagram below summarizes the empirical performance of some of our MAPF algorithms (solid lines) in comparison to some baseline MAPF algorithms (dashed lines). Success rate is the percentage of MAPF instances solved within a runtime limit of one minute.
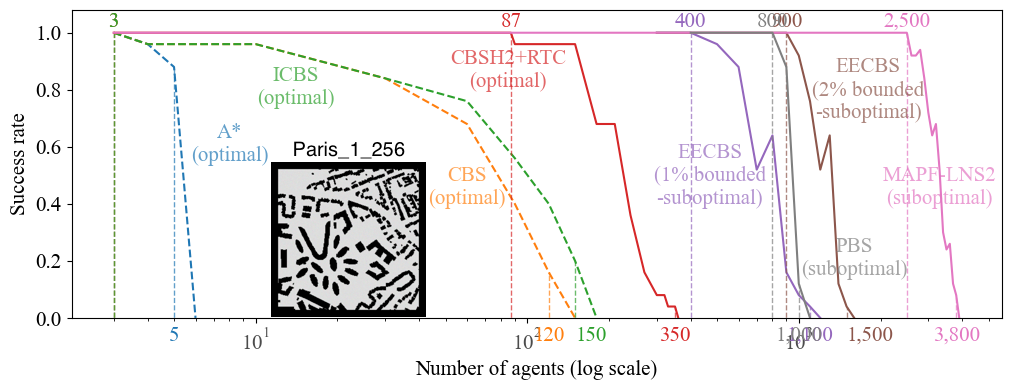
Show more details of this empirical result.
The experiments were conducted on AWS EC2 instances “m4.large” with a runtime of 1 minute. The MAPF instances are the 25 instances in the ``random'' scenario on map ``Paris_1_256'' from the MAPF benchmark suite. The details of each MAPF algorithm are as follows.- A* is a vanilla A* algorithm that searches the joint-state space of the agents.
- CBS is from [Sharon et al AAAI'12]. Check out the code here.
- ICBS is CBS with the conflict prioritization technique from [Boyarski et al IJCAI'15]. Check out the code here.
- CBSH2-RTC is ICBS with the WDG heuristic from our IJCAI'19 paper, the RTC symmetry reasoning from our AIJ'21 paper, and the bypassing technique from [Boyarski et al IJCAI'15]. Check out the code here.
- EECBS is the most advanced version of EECBS from our AAAI'21 paper plus SIPPS from our AAAI'22 paper. Check out the code here.
- PBS is PBS from our AAAI'19 paper plus SIPPS from our AAAI'22 paper. Check out the code here.
- MAPF-LNS2 is from our AAAI'22 paper. Check out the code here.
Symmetry Reasoning for MAPF
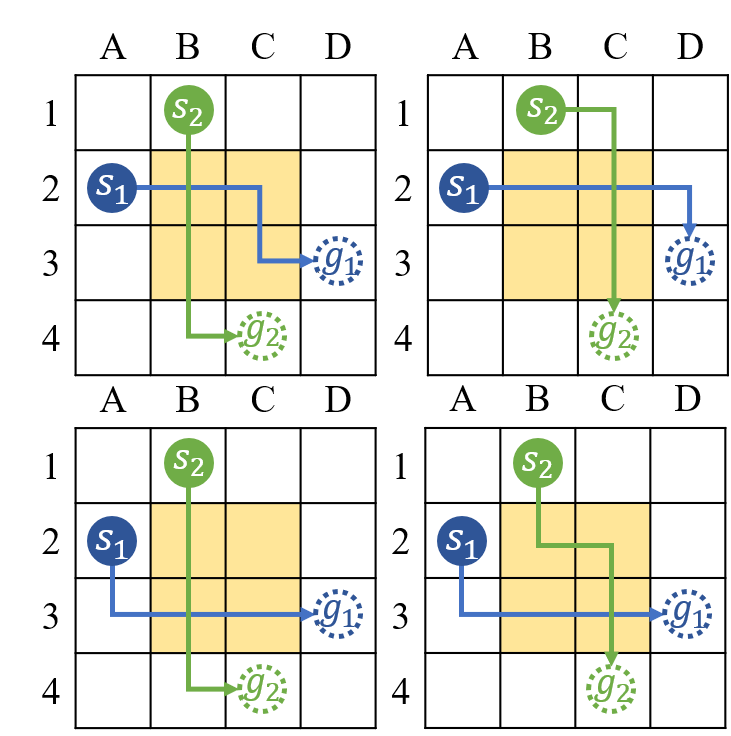 One of the reasons MAPF problems are so hard to solve is due to a phenomena called pairwise path symmetry, which occurs when two agents have many equivalent paths, all of which appear promising, but which are pairwise incompatible because they result in a collision. The symmetry arises commonly in practice and can produce an exponential explosion in the space of possible collision resolutions, leading to unacceptable runtimes for currently state-of-the-art MAPF algorithms that employ heuristic search, such as Conflict-based Search (CBS). To break symmetries, we propose a variety of constraint-based reasoning techniques, to detect the symmetries as they arise and to efficiently eliminate, in a single branching step, all permutations of two currently assigned but pairwise incompatible paths.
One of the reasons MAPF problems are so hard to solve is due to a phenomena called pairwise path symmetry, which occurs when two agents have many equivalent paths, all of which appear promising, but which are pairwise incompatible because they result in a collision. The symmetry arises commonly in practice and can produce an exponential explosion in the space of possible collision resolutions, leading to unacceptable runtimes for currently state-of-the-art MAPF algorithms that employ heuristic search, such as Conflict-based Search (CBS). To break symmetries, we propose a variety of constraint-based reasoning techniques, to detect the symmetries as they arise and to efficiently eliminate, in a single branching step, all permutations of two currently assigned but pairwise incompatible paths.
Highlights: The addition of the symmetry-reasoning techniques proposed in [3] can reduce the number of expanded nodes and runtime of the optimal algorithm CBS by up to 4 orders of magnitude and thus can handle up to 30 times more agents than possible before within one minute.
Relevant publications: [1] rectangle symmetry, [2] corridor and target symmetries, [3] generalized rectangle, target, and corridor symmetry reasoning, [4] automatic symmetry reasoning by mutex propagation (ICAPS’20 outstanding student paper), [5] mutex propagation for SAT-based MAPF, [6] improved mutex propagation, [7] symmetry reasoning for k-robust MAPF, [8] symmetry reasoning for agents of different shapes, [9] symmetry reasoning for train-like agents, [10] target symmetries used for MAPF with precedence constraints, and [11] symmetry reasoning with bounded-suboptimal CBS.
Heuristics for MAPF with Conflict-Based Search
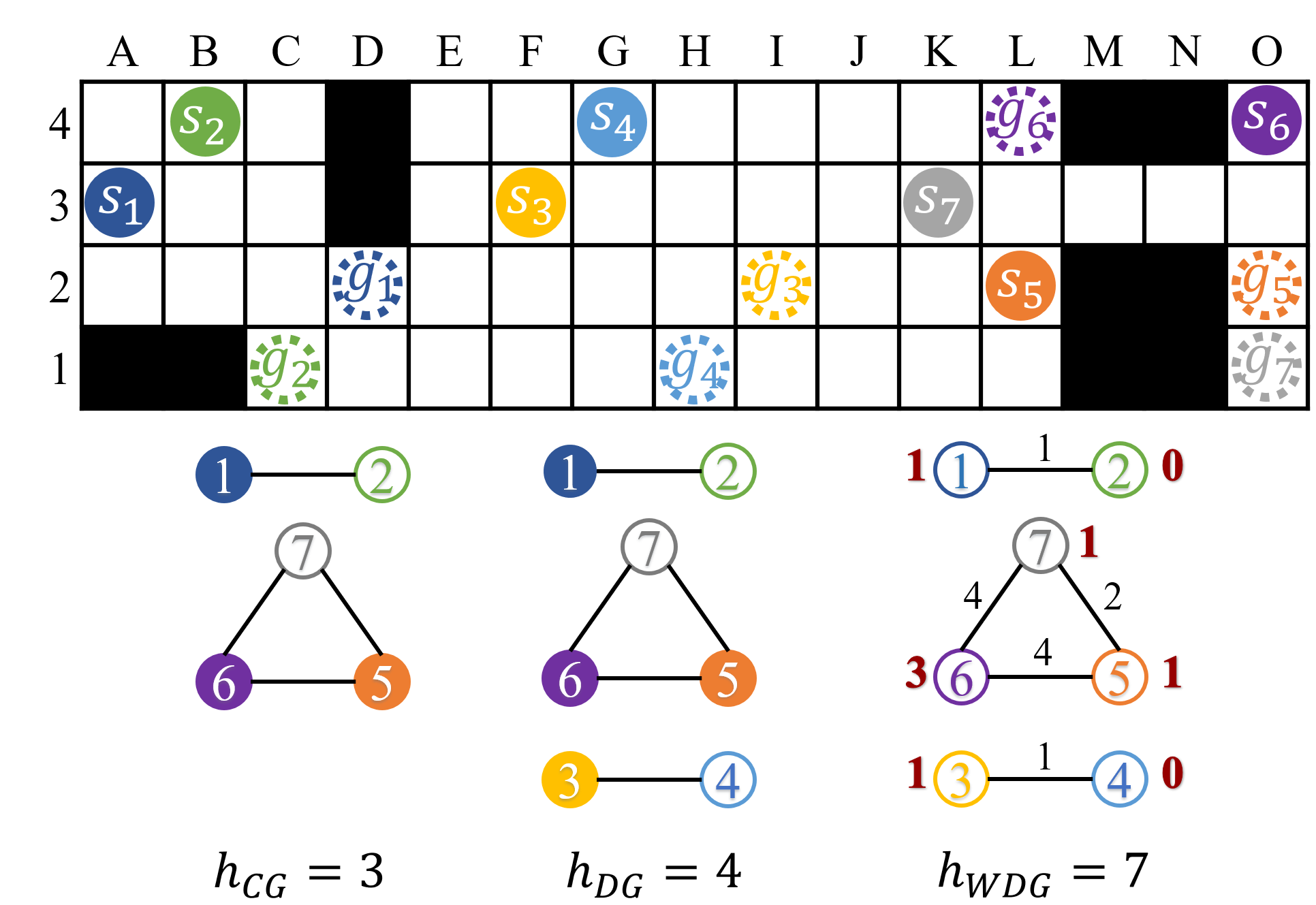 Conflict-Based Search (CBS) and its enhancements are among the strongest algorithms for MAPF. However, existing variants of CBS do not use any heuristics that estimate future work. Introducing admissible heuristics to guide the high-level search of CBS can significantly reduce the size of the CBS search tree and its runtime. Introducing more informed but potentially inadmissible heuristics to guide the high-level search of bounded-suboptimal CBS with Explicit Estimation Search can further reduce the size of its search tree and its runtime.
Conflict-Based Search (CBS) and its enhancements are among the strongest algorithms for MAPF. However, existing variants of CBS do not use any heuristics that estimate future work. Introducing admissible heuristics to guide the high-level search of CBS can significantly reduce the size of the CBS search tree and its runtime. Introducing more informed but potentially inadmissible heuristics to guide the high-level search of bounded-suboptimal CBS with Explicit Estimation Search can further reduce the size of its search tree and its runtime.
Highlights: The addition of the admissible heuristics proposed in [2] can reduce the number of expanded nodes and runtime of CBS by up to a factor of 50 and thus can handle up to 3 times more agents than possible before within one minute. The bounded-suboptimal MAPF algorithm proposed in [4] can find solutions that are provably at most 2% worse than optimal with 1,000 agents in one minute, while, on the same map, state-of-the-art optimal algorithms can handle at most 200 agents.
Relevant publications: [1] CG heuristic for CBS, [2] DG and WDG heuristics for CBS, [3] generalized WDG heuristic for CBS with large agents, and [3] inadmissible heuristic for bounded-suboptimal CBS.
Large Neighborhood Search for MAPF
 Sometimes, we are interested in a good solution but not necessarily a proof of how good the solution is. Since providing optimality proofs is computationally expensive, We develop Large Neighbor Search (LNS) algorithms that repeatedly replan paths for subsets of agents via prioritized planning. They give up optimality guarantees but find near-optimal solutions for thousands of agents in practice, solve 80% of the most challenging instances in the MAPF benchmark suite (while previously the best suboptimal algorithms solve at most 65%), and improve the solution quality by up to 36 times.
Sometimes, we are interested in a good solution but not necessarily a proof of how good the solution is. Since providing optimality proofs is computationally expensive, We develop Large Neighbor Search (LNS) algorithms that repeatedly replan paths for subsets of agents via prioritized planning. They give up optimality guarantees but find near-optimal solutions for thousands of agents in practice, solve 80% of the most challenging instances in the MAPF benchmark suite (while previously the best suboptimal algorithms solve at most 65%), and improve the solution quality by up to 36 times.
Relevant publications: [1] LNS for improving solution quality, [2] LNS for increasing success rates, [3] LNS for railway planning and replanning, [4] machine learning guided LNS for MAPF, and [5] LNS for multi-agent task and path planning.
Learning-Guided Planning
Machine Learning (ML) can complement the search algorithms and boost their performance by automatically discovering policies that are better than the hand-crafted ones and tailoring the randomized heuristics to the instances at hand. Examples include learning to generate priority orderings for prioritized planning and to select subsets of agents and determine the stopping criterion for LNS.
Relevant publications: [1] ML-guided LNS for MAPF, [2] ML-guided prioritized planning for MAPF, and [3] combining RL with LNS.
Learning individual policies for agents
An appealing alternative approach to using heuristic search methods is to use machine learning to directly learn a MAPF policy for each agent. Depending on implementation, this could theoretically be decentralized (e.g. each agent running its own policy and communicating with a small subset of neighboring agents), fast (just the time required for a neural network inference), and result in efficient paths.
[1] Collision sheilding for learning-based MAPF, [2] Imitation learning for MAPF, and [3] Imitation learning for large-scale lifelong MAPF.
